CSAPP(2)-信息的表示与处理
CSAPP第二章总览
视频学习与思考
数字的位级表示
——everything is bits
==用有限的位组合形式表示在数域中无限扩张的数==
bit is 0 or 1
4 bits可表示为十六进制
二进制清晰稳定,简单易存储
1010
1011 B
1100
1101 D
1110
1111 F
位级运算
关于布尔代数

位操作:

如上,当我们操作连续的bits时,可看作是对每个比特位进行布尔操作
你可以直接在C语言中执行这些低级别的位操作
*虚拟电子空间是由机器字长决定的
 上例是一种隐式的表示数值集合的方式:
上例是一种隐式的表示数值集合的方式:
对这些位进行从右向左编号,1的位置表示这个位置上所代表的数字在此集合中,0则表示不在
从上图中可以看出:
& 类似集合的交
| 类似集合的并
^ 类似集合的异或并
~ 类似集合的补集
位表示集合
注意区分&和&&,|和||,~和!,前者是位操作,后者是条件判断

最后一行可以测试空指针,如果是0或null,就能避免对空指针的访问
位移
左移
位整体向左移w位(前w位抹去,后补w个零)
右移
逻辑右移
位整体向右移w位(前w位补零,后w位抹去)
算术右移
位整体向右移w位(前w+1位若为1,前w位补1,否则补零;后w位抹去)
**PS:**实际上位移量是通过计算k mod
w得到的。不过==这种行为对于C程序来说是没有保证的==,所以应该保持位移量小于待移位值的位数。另一方面,Java特别要求位移数量应该按照我们前面所讲的求模的方法来计算。
==向左移动负数可能会导致结果逻辑右移==
整数表示
无符号数

无符号数的二进制表示有一个很重要的属性,也就是每个介于0~2^n-1之间的数都有唯一一个n位的值编码。

补码

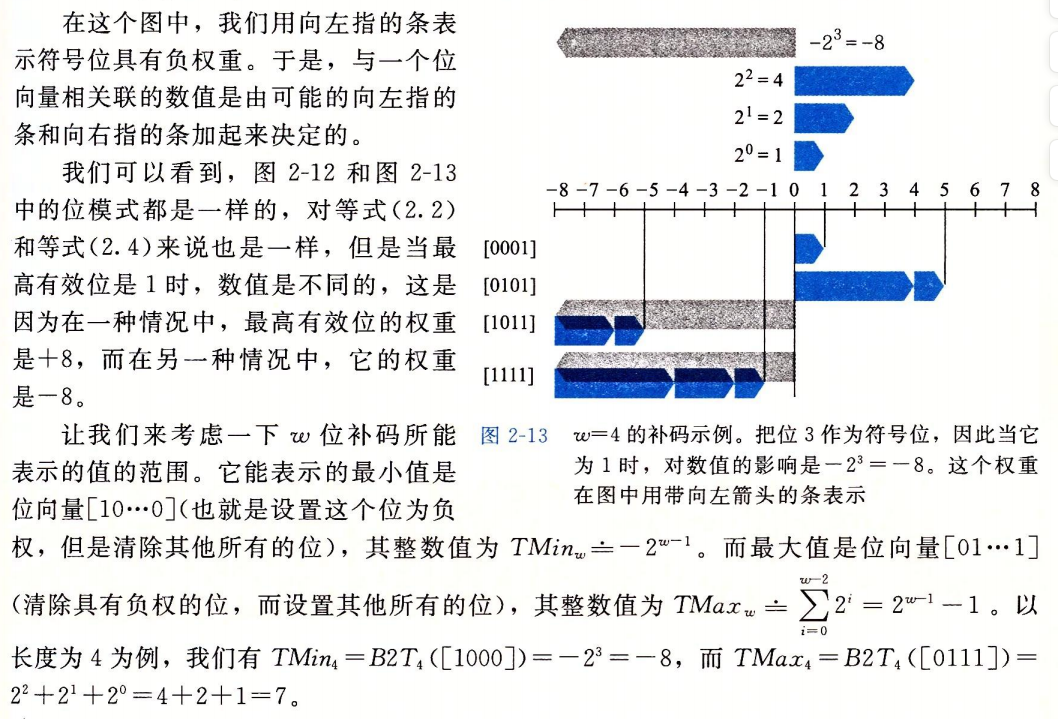
补码范围不对称
C语言用补码表示有符号整数

最高位有时称为符号位,在补码中,如果它为1,就是负数。
所有位为1的是-1
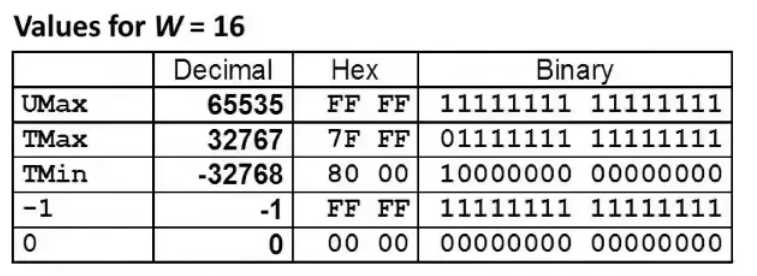
|TMax|=|TMin|-1
因为 -TMin=TMax+1=0x7FFF+1=0x8000=TMin
所以 ==-TMin=TMin==
UMax=2*TMax+1
==int 会被转换为 unsigned!!!==
i-sizeof(int)>=0 是无符号之间的比较
补码的产生:
计算机的ALU是由加法单元实现的,而加法只会产生进位,而不需要考虑借位。而我们现实中的减法运算则会产生借位操作。因此在实现减法的时候为了复用加法器,让加法器可以执行减法操作,就需要消除想办法消除减法的借位行为。
而最大的数在进行减法运算时刚好不需要借位,因此我们在进行减法运算的时候先加一个最大的数(我们假设为MAX),再减去一个最大的数,然后根据结合率,我们先使用最大的数与减数进行计算,将结果与被减数相加,就可以消除减数与被减数之间的借位了,但是最后减去MAX的时候还是会产生借位。因此我们考虑MAX + 1,因为MAX进位后产生的是1个1,剩余的全是0,这样就可以把借位全部消除了。==?==
因此A - B 就转换为 A +(MAX - B)+ 1 - (MAX + 1)的形式。
MAX-B就叫做X的补码(X为该进制下的最大数字,比如二进制下X为1,十进制下X为9),即如果是在十进制下计算A-B,则MAX-B的结果叫做B对9的补码,如果是二进制下计算,则MAX-B的结果叫做B对1的补码。
‘10’后面跟位数-1个0是MAX + 1的结果,所以==MAX-B + 1叫做B对‘10’的补码==,也就是我们在计算机课本中常见的补码的概念。
由于二进制的特殊性,二进制下MAX-B可以简单的转换为将B的各位取反,因此二进制下”补码”的计算,是将B的各位取反后加1。
由上面的分析我们可以知道B的”补码”可以当作-B来使用,只要在最后减去一个MAX+1即可,即在三位下最后减去‘1000’,四位下减去‘10000’。
但在上面需要注意,如果被减数小于减数,即产生一个为负的结果时, A +(MAX - B)+ 1 位数与原来相同,而 (MAX + 1)是多一位的,例如100-150, 100 +(999 - 150)+ 1结果是950,而 (999 + 1)是1000,此时虽然950与000的计算不需要借位,但是1000比950多了一个最高位,因此还是需要借位才能继续运算。
在这种情况下,我们再更换一下思路,使用减数减去被减数,得到结果再取负即可。即将A-B转换为B-A,再用上面的方式来消除借位。
补码的应用:
补码可以表示负数,因此8位二进制所表示的256种变化中有一半要用于去表示补码,即负数。而最高为1之后的数字刚好是128-256,因此这部分表示为补码的话刚好是127-1的补码,因此00000001-01111111的含义不变,表示1-127,而10000000-11111111的含义变为其所表示的补码的含义,即-128到-1(需要减100000000),00000000表示0。
最重要的是,由于计算机只能存储8位,所以MAX + 1超出8位限制,因此相当于减00000000,所以在计算机内可以直接补码视为负数,而不需要再去减MAX+1,因为此时MAX + 1相当于计算机中的0,虽然在现实中相当于10000。(溢出)
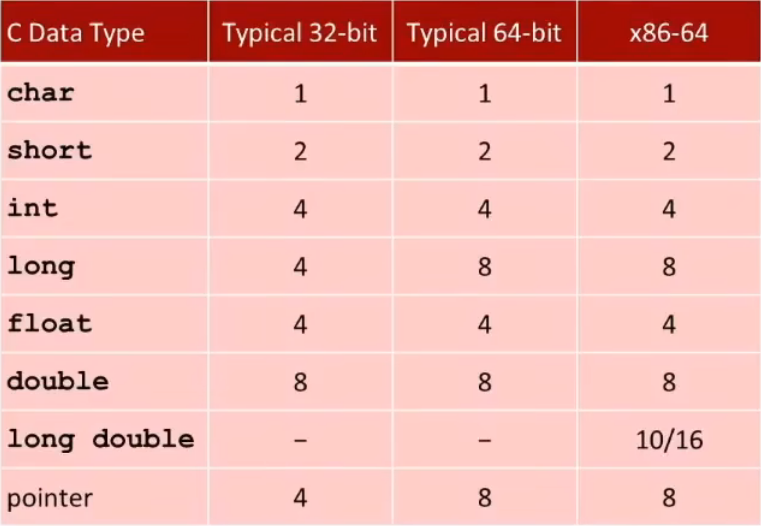
C语言标准只指定了每种数据类型的最小范围,而不是确定的范围。虽然我们可以选择与大多数机器上的标准表示兼容的数据类型,但是这也不能保证可移植性。
使用宏能保证:不论代码是如何被编译的,都能生成正确的格式字符串。
Java标准是非常明确的。它要求采用补码表示,取值范围与图2-10中64位的情况一样。
在Java中,单字节数据类型称为byte,而不是char。这些非常具体的要求都是为了保证无论在什么机器上运行,Java程序都能表现地完全一样。
C和C++有无符号都支持,Java只支持有符号数
有无符号数之间的转换
C语言允许在各种不同的数字数据类型之间做强制类型转换。C是少数unsigned是明确的数据类型的语言之一
强制类型转换的结果保持位值不变,只是改变了解释这些位的方式。
-12345的16位补码表示与53191的16位无符号表示是完全一样的。将short强制类型转换为unsigned short改变数值,但是不改变位表示。
无符号形式的4294967295(UMax32)和补码形式的-1的位模式是完全一样的。将unsigned强制类型转换成int,底层的位表示保持不变。
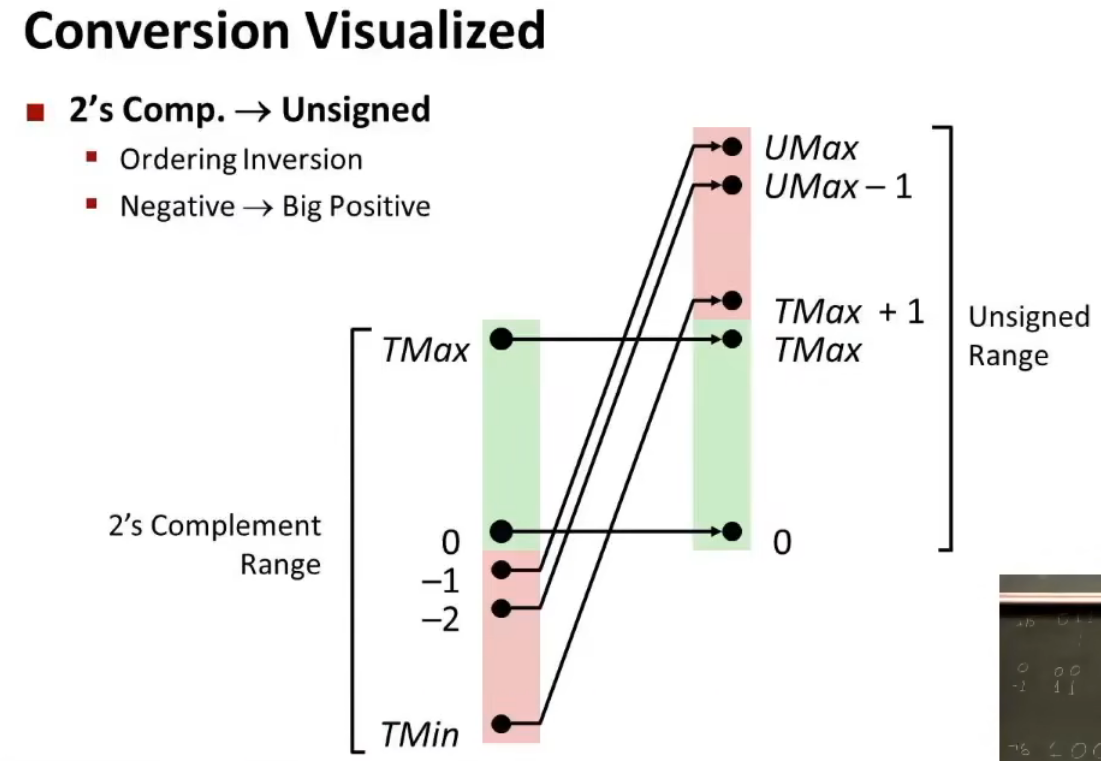
1+UMax=2^w
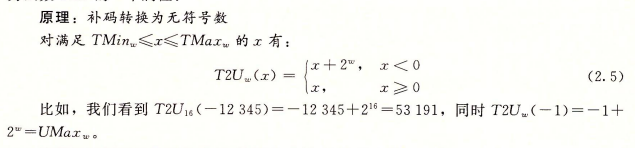
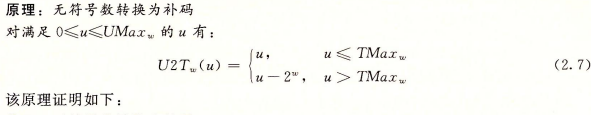
对于在范围O≤x≤TMaxw之内的值x而言,我们得到T2Uv(x)=x和U2Tw(x)=x。也就是说,在这个范围内的数字有相同的无符号和补码表示。对于这个范围以外的数值,转换需要加上或者减去2^w。
关于C语言中的整数问题
大多数数字都默认为是有符号的。例如,当声明一个像12345或者0x1A2B这样的常量时,这个值就被认为是有符号的。要创建一个无符号常量,必须加上后缀字符‘u’或者‘u’,例如,12345U或者0x1A2Bu。
在一台采用补码的机器上,当从无符号数转换为有符号数时,效果就是应用函数U2Tw,而从有符号数转换为无符号数时,就是应用函数T2U,其中w表示数据类型的位数
==当执行一个运算时,如果它的一个运算数是有符号的而另一个是无符号的,那么C语言会隐式地将有符号参数强制类型转换为无符号数,并假设这两个数都是非负的,来执行这个运算。==就像我们将要看到的,这种方法对于标准的算术运算来说并无多大差异,但是对于像<和>这样的关系运算符来说,它会导致非直观的结果。
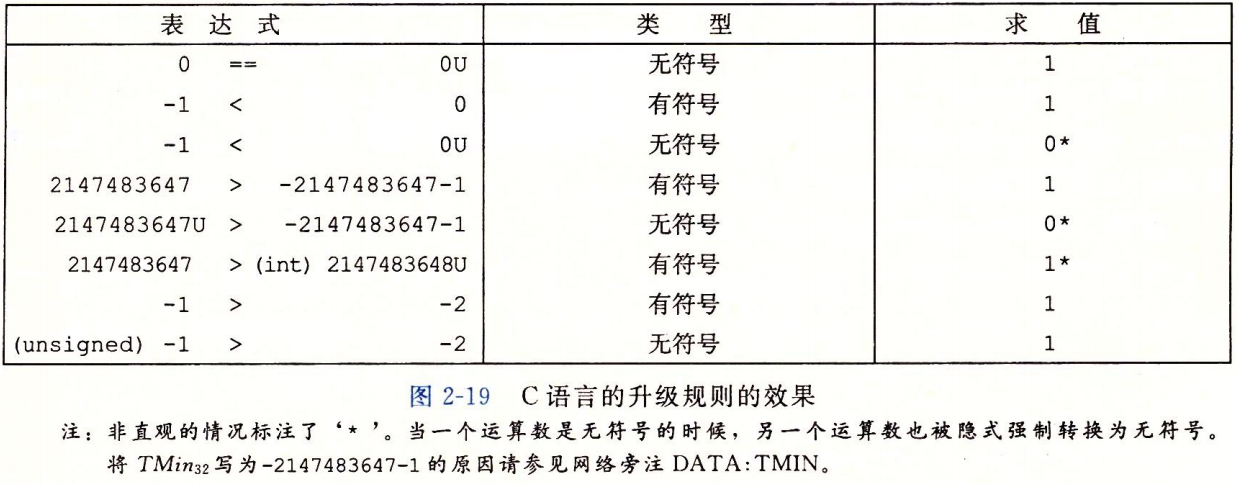
首先判断数有无符号,避免隐式转换
如果用无符号的0与-1比较,会得到相反的结果

扩展位数

1110===-8==+4+2=-2
11110===-16+8==+…=-2
……
数字截断


截断补码要关注第一位的0 1区别
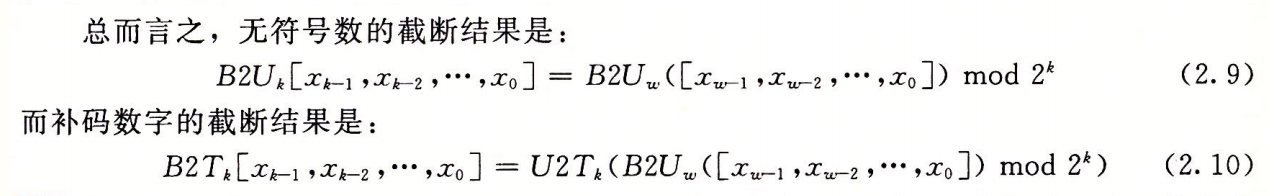
建议

避免这类错误的一种方法就是绝不使用无符号数。实际上,除了C以外很少有语言支持无符号整数。
Java只支持有符号整数,并且要求以补码运算来实现。正常的右移运算符>>被定义为执行算术右移。特殊的运算符>>>被指定为执行逻辑右移。
当我们想要把字仅仅看做是位的集合而没有任何数字意义时,无符号数值是非常有用的。例如,往一个字中放入描述各种布尔条件的标记(flag)时,就是这样。地址自然地就是无符号的,所以系统程序员发现无符号类型是很有帮助的。当实现模运算和多精度运算的数学包时,数字是由字的数组来表示的,无符号值也会非常有用。
整数运算
计算机的有限性会导致当数字大到所能表示的最大值后,就会溢出
无符号加法
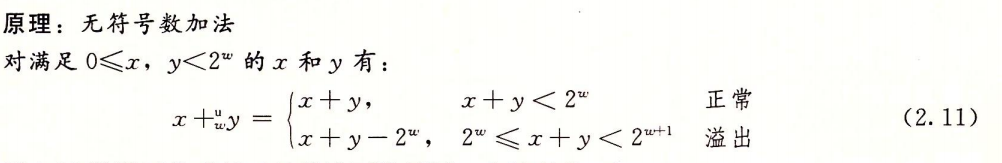
简单来说就是当产生溢出时会丢弃最高位(截断),程序没有任何异常
本质为模运算
补码加法
不发生溢出的情况下,正常进行运算就可以获得正确的结果;发生溢出,负数相加可能获得正数或其他任何数
正数相加会得到负数
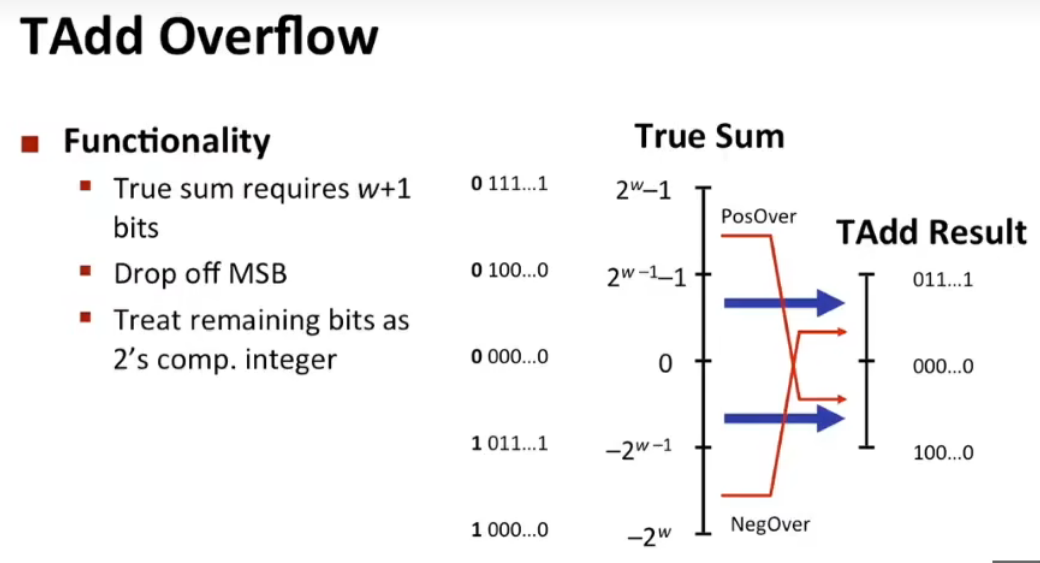
运算溢出(空间耗尽)
50000*50000=?
浮点数(float)
近似表示(舍入问题)
1e20-(1e20+3.14)=0
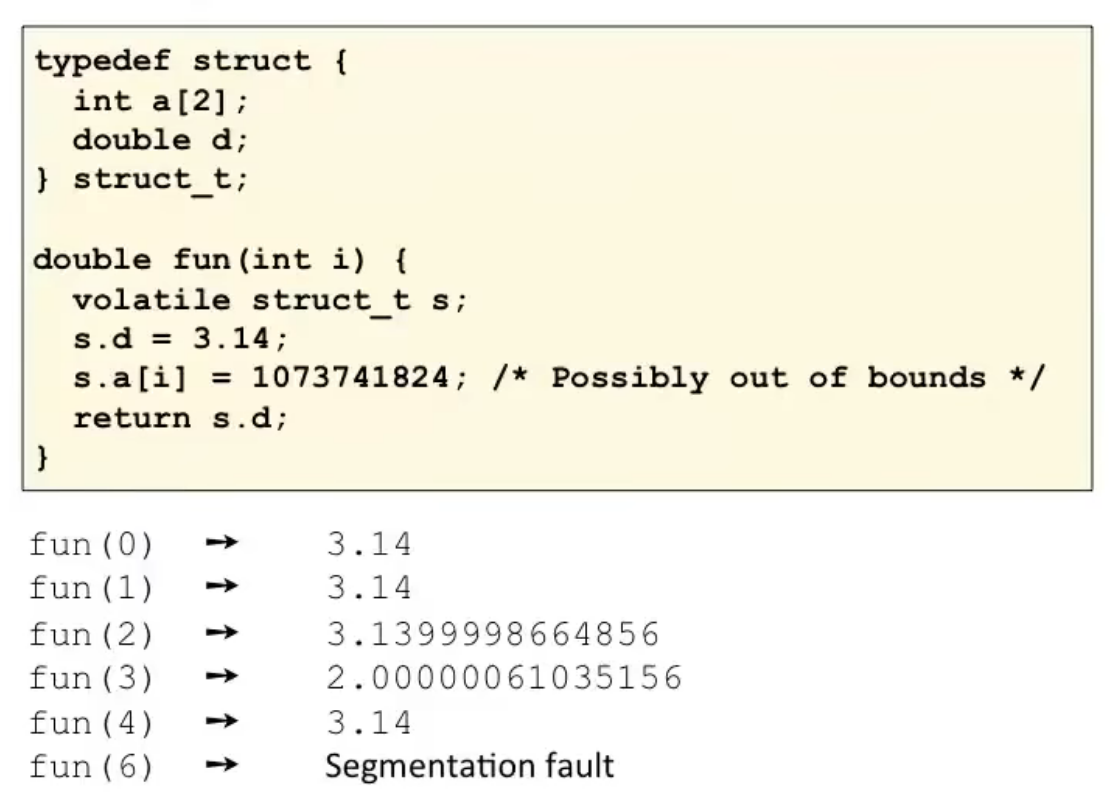
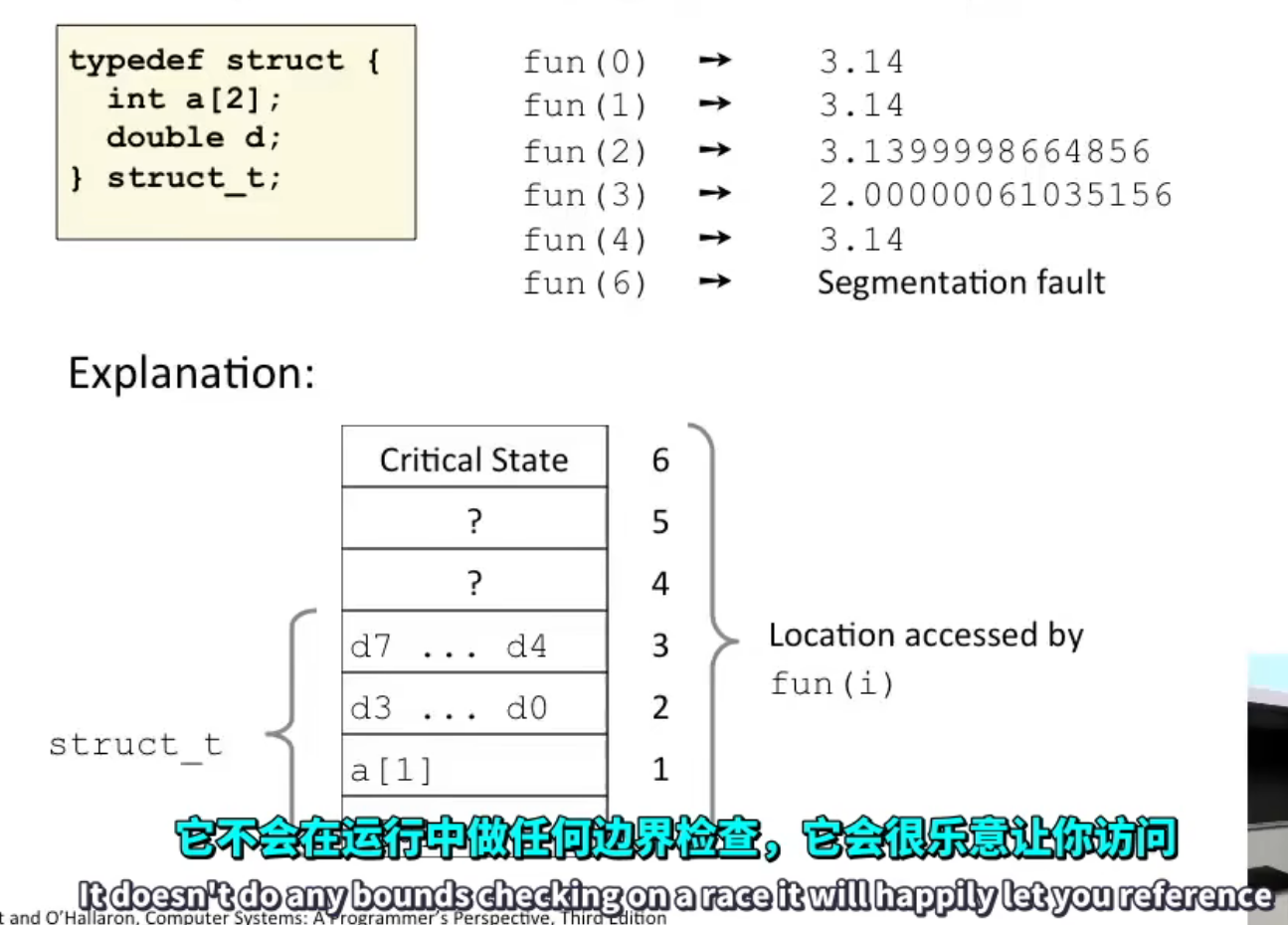
易写出非法的代码

不同的内存访问模式对计算机性能优化有巨大效果(与内存层次结构的缓存有关)